Komputer kwantowy posiadający n elementów potrafi zapamiętać i w jednym cyklu przetworzyć 2ⁿ informacji. Nie jak zwykły komputer tylko od 4 do 128 bitów naraz, a więc dzięki niemu policzymy miliony razy szybciej.

Maszyna Turinga – problemy nierozwiązywalne

Wiara w możliwości komputera bywa złudna. Już w 1936 roku Alan Turing podał w słynnym artykule problem arytmetyczny, którego żaden komputer nie jest w stanie policzyć.

Alan Turing w latach 30. XX wieku – Źródło Wikipedia

Szczerze mówiąc to był jedyny cel tego artykułu. Turing chciał udowodnić, że istnieją problemy matematyczne, których matematyka nie jest w stanie rozstrzygnąć. Komputer, a ściślej jego matematyczny model, powstał tu jedynie jako narzędzie mające wykazać nierozstrzygalność. To znaczy, że nie da się stworzyć żadnej systematycznej metody obliczeniowej dla pewnego problemu, który wymyślił Turing. Od tego czasu tzw. problemów nierozstrzygalnych namnożyło się wiele, co wcale nie znaczy, że już zupełnie nie da się ich „ugryźć”, ale wymaga to wielu zabiegów, których efekt nie zawsze jest pewny. A ten „uboczny produkt” pracy, matematyczny model komputera, zyskał w literaturze miano „Maszyny Turinga”.

Schemat maszyny Turinga – Źródło EDUX

Po dziś dzień każdy szanujący się student informatyki musi ją dobrze znać .
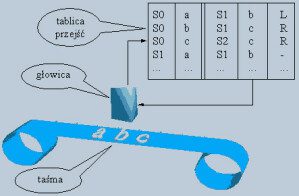
Maszyna Turinga dysponuje nieskończoną taśmą, na której głowica może zapisywać i z której odczytywać różne symbole przesuwając taśmę w przód lub w tył. O tym co maszyna robi z taśmą decyduje tablica przejść na podstawie aktualnego stanu maszyny i symbolu pod głowicą. Tablica przejść zmienia też stan maszyny. Pomimo, że Maszyna   Turinga różni się zarówno od współczesnego sprzętu komputerowego jak też bardzo już rozwiniętych jezyków programowania to ten teoretyczny model jest równoważny każdemu dawnemu i współczesnemu komputerowi z wyjątkiem … komputera kwantowego.

Złożoność obliczeniowa czyli klasyfikacja trudności problemów 

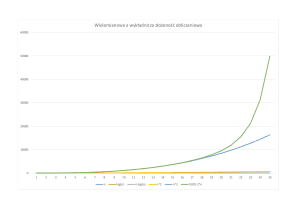
Po wielu latach od tego odkrycia zaczęto badać wydajność programów komputerowych i algorytmów (czyli ich abstrakcyjnych wzorców). Okazało się, że dobrym wskaźnikiem wydajności jest wzór uzależniający czas obliczeń od wielkości danych wprowadzanych do programu. Najszybsze programy liczyły z czasem oznaczanym jako O(n) – co oznaczało, że czas obliczeń zależał liniowo od wielkości danych. Ale już na przykład prymitywne metody porządkowania danych (tzw. sortowanie) wymagały czasu obliczeń rzędu O(n²) – czyli n do kwadratu. Metody bardziej wyszukane natomiast działały w czasie zależnym przeciętnie od funkcji O(n·log(n)) – a więc funkcji o pośredniej między liniową, a kwadratową złożoności. Są oczywiście również funkcje szybciej rosnące, ogólnie określane mianem wielomianowych. Jeśli jednak zmienna powędruje do wykładnika (np. O(2ⁿ)) to mamy do czynienia z funkcją wykładniczą o diametralnie różnych od wielomianowych własnościach.

Zasadnicza różnica pomiędzy spokojną złożonością wielomianową, a ostro w górę idącą wykładniczą

Funkcje wykładnicze (zielone na wykresie) rosną bowiem tak szybko, że duże problemy wymagałyby na ich rozwiązanie wieków, gdy dla funkcji wielomianowej (żółte i niebieskie na wykresie) przy tym samym n to zaledwie sekundy. Mamy oczywiście na myśli jakieś większe, o praktycznym znaczeniu wielkości n. W trakcie badań okazało się, że nie wszystkie problemy są z gruntu skazane na algorytmy wykładnicze. Są też takie problemy, dla których nie da się tego udowodnić, ale nie znaleziono też jak dotąd algorytmu wielomianowego. Te problemy zaliczamy do klasy NP-zupełnych, gdyż są one ze sobą powiązane algorytmami przekształcającymi dane jednego problemu w drugi. Gdyby więc udało się znaleźć algorytm wielomianowy dla choćby jednego problemu z tej klasy to i pozostałe dałoby się rozwiązać w czasie wielomianowo-zależnym od rozmiaru problemu. Jednak nadzieje na takie rozstrzygnięcie są coraz mniejsze, bo było już tyle zakończonych niepowodzeniem prób znalezienia takich algorytmów.

Komputer kwantowy – pogromca złożoności wykładniczej?

Efektywne rozwiązywanie problemów NP-zupełnych na klasycznych komputerach zdaje się być przesądzone negatywnie. Natomiast komputery kwantowe dają zupełnie nowe możliwości. Przykładowo weźmy trudny problem badania czy dana liczba jest pierwszą (albo próby znajdowania jej wszytkich możliwych podzielników). Gdy liczba badana ma wartość x wymaga danych o wielkości n=log₁₀x (t o jest tylu znaków wymaga zapisanie liczby o wartości x), dla których należy wykonać x operacji dzielenia (przez każdą z liczb od 2 do x-2), a więc jak wynika ze wzoru z logarytmem x= 10ⁿ operacji. Dla tego właśnie problemu znaleziono algorytm działający na komputerze kwantowym znajdujący podzielniki w czasie ograniczonym wielomianem.

Można zadać pytanie skąd taki zaskakujący wynik? Otóż komputer kwantowy wykonuje obliczenia nie na bitach a na qbitach. Każdy qbit może nie jak bit przechowywać albo 0 albo 1 lecz przechowuje informację o tym w jakiej części to jest 0 a w jakiej 1. Ważne jest przy tym powiązanie z innymi qbitami danej maszyny. Mając n qbitów komputer kwantowy może przechowywać jednocześnie 2ⁿ wektorów stanów bitów o długości n. I tak na przykład dla n=3 będą to maksymalnie: 0-0-0, 0-0-1, 0-1-0, 0-1-1, 1-0-0, 1-0-1, 1-1-0 oraz 1-1-1. I co ciekawe w jednym cyklu wykonywać przetwarzanie wszystkich tych wektorów naraz. Przy większych ilościach qbitów daje to olbrzymie przyspieszenie obliczeń.

Komputer kwantowy – wciąż niedoskonały

Richard Feynman – Źródło Wikipedia
Paine Mansion Woods 1984 copyright Tamiko Thiel

Na koniec trzeba wyraźnie sobie powiedzieć, że współczesne próbne komputery kwantowe mają wiele wad uniemożliwiających efektywne ich wykorzystanie w zadaniach praktycznych. Np. działania wielu elementów komputera obarczone jest błędami statystycznymi, których eliminacja do rozsądnego poziomu wymaga powtarzania obliczeń. Trudne jest też odczytywanie wyników obliczeń, bowiem takie próby powodują zniszczenie całego zbioru wyników i sprowadzenie ich do jednego z wielu wyznaczonych.

Jeden wielkich fizyków XX wieku Richard Feynman rzucił kiedyś luźną uwagę  na temat niemożności śledzenia przemian kwantowych zwykłymi komputerami. Przeistoczyła się ona najpierw w namacalne dowody wskazujące na możliwość pokonania tej niedoskonałości zwykłych komputerów, a potem wiele nowatorskich konstrukcji komputerów kwantowych zdolnych tego dokonać.

W końcu w pracy [11] zaproponowano Kwantową Maszynę Turinga, która miała lepiej oddawać naturę obliczeń na tych nowych urządzeniach.

Bibliografia

1. Alan Turing: On computable numbers, with an application to entscheidungs problem, 1936.
2. Garey, M. R.; Johnson, D. S., Victor Klee, ed. Computers and Intractability: A Guide to the Theory of NP-Completeness. A Series of Books in the Mathematical Sciences, San Francisco, Calif.: W. H. Freeman and Co., 1979.
3. Jacek Błażewicz Złożoność obliczeniowa problemów kombinatorycznych, Wydaw. Nauk.-Techn., Warszawa, 1988.
4. Andrew Hodges, Wiktor Bartol: Enigma: życie i śmierć Alana Turinga, Warszawa: Prószyński i S-ka, 2002.
5. Paweł Maretycz Wielki sukces IBM – komputer kwantowy firmy bije kolejne rekordy NEWSY ,, 05-02-2021.
6. Firma Ion pokazała najbardziej wydajny na świecie komputer kwantowy
7. Google potwierdza supremację kwantową. 10 tys. lat obliczeń w 200 sekund,  https://dzienniknaukowy.pl/nowe-technologie/google-potwierdza-supremacje-kwantowa-10-tys-lat-obliczen-w-200-sekund
8. IBM ogłasza kwantowy przełom
9. Jak kwantowość zmieni przyszłość
10. Inne trudne obliczeniowo problemy rozwiązywane przez współczesną informatykę jeszcze bez komputerów kwantowych
11. David Deutsch „The fabric of reality”, Penguin Books, 1997, Hrmondsworth, Middlesex, England.